ワカるデキる　対数（３）　～対数は指数と兄弟関係～

　2+2+2 を略して 2\times3 と書くように、 2\times2\times2 も略して 2^3 と書くことができます。このとき、もとになる数字 “2” を「底（てい）」、右肩の小さな数 “3” のことを「指数」と呼びます。
　言いかえれば、2^3=8 とは「”2″ という底を “3”乗 すると、”8″になる」という意味です。
　これをさらに言いかえれば、「”2″ という底が “8”という数字（真数）になるのは、”3″乗した場合（対数）である」となります。
　これを数式で表すと、\log_2 8=3 と書きます。この式では “2” が底、 “8” が真数、 “3” が対数になります。

　　指数： 2^3=8　　対数： \log_2 8=3

　さて、前回の話の中で、 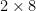2\times8 の数字を暗号化して足し算にすれば、 1+3=4 となり、数字化すれば 16 になる、と述べました。これを指数で表すと、 2^1\times2^4=2^{1+4}=2^5 という形になります。
　同様に、これを対数で表すと、 \log_2 8 + \log_2 16 = \log_2 (8\times16) =4 という形になります。

　　指数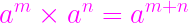： a^m \times a^n=a^{m+n}

　　対数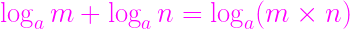： \log_a m + \log_a n = \log_a (m \times n)

　同様に以下の公式も成り立ちます。

　　指数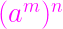： (a^m)^n

　　対数： \log_a m^n = n\log_a m

　このように、指数と対数は対応しながら考えるとわかりやすいですね。
　ところで、ここで、素朴な疑問。

　対数ってそんなに便利？　なぜ、対数が必要なのかわかんない！

　そうだよね、わかる、わかる、その気持ち！　でも、もう少し我慢して、この対数の基礎を勉強しよう！　そのうち、対数の便利さにきっと気付くよ！
　→ 対数（１）　→ 対数（２）　→ 対数（３）　→ 対数（４）　→ 対数（５）　→ 対数（６）