ワカるデキる 対数(5) ~3の33乗は何桁ですか?~
では、今までの知識を応用して問題を解いてみよう!
この問題の意味をよく考えてほしい。ポイントは「何桁の数字か?」という部分である。前回も述べたが、桁数を表すのに “10” を底とした指数で表現することになるのだ。すなわち、この問題のポイントは 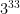 という数字を、”10″ を底とした指数で示す部分にあるのだ。
という数字を、”10″ を底とした指数で示す部分にあるのだ。
よって、この問題を、 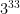 は、”10″ という底の、何乗ですか? と読み替える。そうすると、これを
は、”10″ という底の、何乗ですか? と読み替える。そうすると、これを  という数式で表現できるのだ!
という数式で表現できるのだ!
さて、以前学習した公式  を使って以下のように変形する。
を使って以下のように変形する。
ここで なので、
なので、
ということで、 という数字が出てきたのだが、これは何を意味するかといえば、
という数字が出てきたのだが、これは何を意味するかといえば、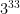 は、
は、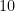 の
の  乗だということなんだ。
乗だということなんだ。
というわけで、おおよその数が「数京」だということがわかりましたね。このように、大体の数、桁数なんかを考える上で、対数は非常に便利なわけです。
でも、最初のヒト桁目が “1” “9” かで、ずいぶん違いますよね? ん~ん、なんとか、ヒト桁目を類推出来ないでしょうか? では、そこは次回勉強しましょう!

