ワカるデキる　対数（６）　～対数の便利さ～

　さて、前回、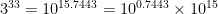 $3^{33} = 10^{15.7443} = 10^{0.7443}\times 10^{15}$ となることをお話ししました。

　ところで、この 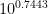$10^{0.7443}$ はどのくらいの数なのでしょうか？

　以前、次のような公式をお話ししました。

$\log_a m + \log_a n = \log_a (m \times n)$

　当然、掛け算が足し算になるならば、割り算は引き算になるので、以下のようになります。

$\log_a m - \log_a n = \log_a (m \div n)$

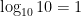　また、ここで、 $\log_{10}2=0.3010$ 、 $\log_{10}3=0.4771$ であり、 $\log_{10}10=1$ になります。（ 10 を何乗すれば 10 になるかといえば、1乗ですからね。）

　すると、以下のようになりますね。

$\log_{10} 2 =0.3010$

$\log_{10} 3 =0.4771$

$\log_{10} 4 =\log_{10}(2\times2) =\log_{10}2 + \log_{10}2 =0.3010+0.3010+=0.6020$

$\log_{10} 5 =\log_{10}(10\div2) =\log_{10}10 - \log_{10}2 =1-0.3010+=0.6990$

$\log_{10} 6 =\log_{10}(2\times3) =\log_{10}2 + \log_{10}3 =0.3010+0.4771=0.7781$

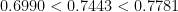　以上から、 $0.6990<0.7443<0.7781$ ですので、”5″ 以上で “6” 以下となります。

　そこで、 $3^{33}$ は、”5″ で始まる16ケタの数、すなわち “約５京” となるのです！

　大昔の科学者は、このような超巨大数の計算（例えば７の１００乗とか）の計算をするのに、数年、下手をすれば一生をかけたことすらあったのですが、この対数のおかげで、数分で計算できるようになるのです！　便利でしょ？

　さて、その上で、次の写真を見ながら、大笑いして、このお話を終わりにしましょう！　またどこかで続きをするかもしれませんがね・・・