サルでもわかる量子論 第6回 ~電子軌道も とびとび!~
第6回 ボーアの電子モデル ~電子軌道も とびとび!~
プランクが、古典物理学を覆す「量子論」の誕生を告げた生みの親であるとすれば、育ての親が、ニールス・ボーアである。
 兄ニールス・ボーアは物理学者であり、弟ハラルド・ボーアは数学者であった。そして、この兄弟は、サッカーの兄弟選手としても全欧に知られていた。特に弟ハラルド・ボーアは、ロンドンオリンピックに出場して、デンマークに銀メダルをもたらした、文武両道実写版の男である。兄ニールス・ボーアも、オリンピックの予備選手にはなったのだが、サッカーの試合で失点する度に「ニールスはGKなのに頭の中は数学の事でいっぱいだからシュートが止められない」と数学好きと絡めて茶化されて、果てには「紙に数式をメモしてる間にゴールされてしまった」という逸話がジョークとして残っている。
兄ニールス・ボーアは物理学者であり、弟ハラルド・ボーアは数学者であった。そして、この兄弟は、サッカーの兄弟選手としても全欧に知られていた。特に弟ハラルド・ボーアは、ロンドンオリンピックに出場して、デンマークに銀メダルをもたらした、文武両道実写版の男である。兄ニールス・ボーアも、オリンピックの予備選手にはなったのだが、サッカーの試合で失点する度に「ニールスはGKなのに頭の中は数学の事でいっぱいだからシュートが止められない」と数学好きと絡めて茶化されて、果てには「紙に数式をメモしてる間にゴールされてしまった」という逸話がジョークとして残っている。
さて、ボーアはまず以下の2つの点について考えた。(ムズカシいので読み飛ばしていい)
 兄ニールス・ボーアは物理学者であり、弟ハラルド・ボーアは数学者であった。そして、この兄弟は、サッカーの兄弟選手としても全欧に知られていた。特に弟ハラルド・ボーアは、ロンドンオリンピックに出場して、デンマークに銀メダルをもたらした、文武両道実写版の男である。兄ニールス・ボーアも、オリンピックの予備選手にはなったのだが、サッカーの試合で失点する度に「ニールスはGKなのに頭の中は数学の事でいっぱいだからシュートが止められない」と数学好きと絡めて茶化されて、果てには「紙に数式をメモしてる間にゴールされてしまった」という逸話がジョークとして残っている。
兄ニールス・ボーアは物理学者であり、弟ハラルド・ボーアは数学者であった。そして、この兄弟は、サッカーの兄弟選手としても全欧に知られていた。特に弟ハラルド・ボーアは、ロンドンオリンピックに出場して、デンマークに銀メダルをもたらした、文武両道実写版の男である。兄ニールス・ボーアも、オリンピックの予備選手にはなったのだが、サッカーの試合で失点する度に「ニールスはGKなのに頭の中は数学の事でいっぱいだからシュートが止められない」と数学好きと絡めて茶化されて、果てには「紙に数式をメモしてる間にゴールされてしまった」という逸話がジョークとして残っている。さて、ボーアはまず以下の2つの点について考えた。(ムズカシいので読み飛ばしていい)
①原子核の周りには電子が飛び回っている。電子の動きは電流である。電流が変化すると電磁波(光)を発生する(実際に原子は光を発する)。電磁波(光)の発生はエネルギーを失うことである。電子が光を発しながらエネルギーを失えば、その分運動エネルギーが減り、電子の軌道は内側に落ち込み、やがては原子核に吸収されるはずである。しかし、実際には原子は安定して存在している、それはなぜか?
②実は光にはさまざまな波長が混在していることが多く、それを波長ごとに分解したものをスペクトルと呼ぶ。太陽光などはスペクトル分解するとそれぞれの波長の光が連続的に分布する連続スペクトルであるが、水素原子が放つ光をスペクトル分解するとある一定の波長が限定的に分布する線スペクトルになる。それはなぜか?
そしてボーアはこう考えた。「電子は、とびとびの軌道しか取り得ないのではないか」。大変な着想である。プランクは、光のエネルギーがとびとびであることを提唱したのだが、ボーアは、それを電子軌道という思いもよらぬところへ応用した。まさに天才といえよう。
さて、問題は「電子は不連続のとびとびの軌道を取る」と仮定した場合に、上の2つの問題点がクリアできるかどうかである。
①例えてみれば「電子は不連続のとびとびの軌道を取る」ということ決まった線路があるということだ。逆に「電子は連続的に自由な軌道を取る」ということは決まった線路はないということである。電子は、原子核の周りをまわり光を発しながらエネルギーを失っているのであるが、もし線路があればなかなか脱線しにくい。多少エネルギーがなくなっても線路がひかれているので、その線路に沿って同一軌道で走ることになる。これに対して線路がない場合はエネルギー損失に応じて徐々に軌道を変えていってしまう。すなわち、電子軌道の安定性のためには、決まった線路=軌道が必要である。ゆえに「電子は不連続のとびとびの軌道を取る」といえる。
②水素原子が光を発するためにはエネルギーが必要である。そのエネルギーはどこから来るのか。もし「電子は不連続のとびとびの軌道を取る」ならば、外側の軌道から内側の軌道に線路を変更するときに大きなエネルギー放出が必要になる(だから通常は同一軌道で安定している)。つまり外側軌道でまわる方がエネルギーが大きいので、エネルギーが小さい内側軌道に移ると、エネルギーが余る。その余ったエネルギーの差がそのエネルギー分の波長の光子となって放出される。ここで電子の軌道は不連続でいくつかしかない。すると放出するエネルギーの差、そしてそれによって放出される光子の波長も限定されることになる。線スペクトルというのはある一定の波長が限定的に分布する線スペクトルになので、ゆえに「電子は不連続のとびとびの軌道を取る」といえる。
いかがであろう? 見事に問題点がクリアされたではないか!
実は、化学の世界で、原子は陽子と中性子を含む原子核の周りを電子がグルグル回って存在しており(という考え方も実際のところは正しくないのだが、とりあえずこう考えておこう)、その電子の軌道は内側からK殻、L殻、M殻、N殻と呼んでいるのはご存知であろう。これこそ、ボーアが提唱した「電子は不連続のとびとびの軌道を取る」という結論なのである。ここからは、それを数学的に証明してみよう。
電子は原子核の周りをグルグル回っている、これは円運動である。古典力学により円運動する物体は 円の中心に向かう力(向心力)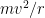 (
(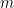 :質量、
:質量、 :速度、
:速度、 :円半径) とあらわすことができる。そしてこの電子の場合円の中心に向かう力は、陽子と電子の間に働く静電気力なので
:円半径) とあらわすことができる。そしてこの電子の場合円の中心に向かう力は、陽子と電子の間に働く静電気力なので 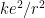 (
(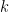 :クーロン定数、
:クーロン定数、 :電気量、
:電気量、 :距離) とあらわすことができる。
:距離) とあらわすことができる。
よって、次のような式になる。
実は、化学の世界で、原子は陽子と中性子を含む原子核の周りを電子がグルグル回って存在しており(という考え方も実際のところは正しくないのだが、とりあえずこう考えておこう)、その電子の軌道は内側からK殻、L殻、M殻、N殻と呼んでいるのはご存知であろう。これこそ、ボーアが提唱した「電子は不連続のとびとびの軌道を取る」という結論なのである。ここからは、それを数学的に証明してみよう。
電子は原子核の周りをグルグル回っている、これは円運動である。古典力学により円運動する物体は 円の中心に向かう力(向心力)
よって、次のような式になる。
次に、ボーアはこう考えた。「電子は不連続のとびとびの軌道を取る」のならば、ある軌道でグルグル回っている時の運動量(円運動をしている運動量なので角運動量と呼ぶ)はある一定の値であるはずだ。そして別の軌道の角運動量な別の値であるはずだ。軌道が別々だから、角運動量も別々。軌道が複数あれば、角運動量も複数ある。ただし、プランクの公式(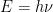 )により、エネルギーは連続量ではなく、必ずプランク定数の倍数になるはずである。そこで電子の角運動量(質量mと速さvと回転半径rを掛け合わせたもの)は、その軌道を一回り(単位ラジアンで一周なので、2π)総合したものは、プランク定数(h)の整数倍(n倍)であると。
)により、エネルギーは連続量ではなく、必ずプランク定数の倍数になるはずである。そこで電子の角運動量(質量mと速さvと回転半径rを掛け合わせたもの)は、その軌道を一回り(単位ラジアンで一周なので、2π)総合したものは、プランク定数(h)の整数倍(n倍)であると。
うん、いまひとつわかりにくい。ひょっとしてボーアにもそれほど明確なイメージがあったかどうかは疑わしいらしい。それでも彼はそれを数式化した。
うん、いまひとつわかりにくい。ひょっとしてボーアにもそれほど明確なイメージがあったかどうかは疑わしいらしい。それでも彼はそれを数式化した。
さてさて、式①と式②を連立して を求めてみよう。でてきた答えがこれだ!
を求めてみよう。でてきた答えがこれだ!
これでn=1の時の半径 を求めるとこうなる。
を求めるとこうなる。
これを代入するとこうなる。
ボーアの電子軌道 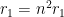
これが意味するものは、原子核の一番近いところにある電子軌道から整数nの2乗に比例して電子軌道は大きくなるということであり、「電子は不連続のとびとびの軌道を取る」ということが証明されるのであった。よかったよかった。
でもボーア本人が知っていたかどうかは定かではないが、もっとよかったことがあるのだ。それは「式②」である。実は、この後に出てくるド・ブロイの物質波の考えによって、この式は別の解釈を与えられることになるのである。
でもボーア本人が知っていたかどうかは定かではないが、もっとよかったことがあるのだ。それは「式②」である。実は、この後に出てくるド・ブロイの物質波の考えによって、この式は別の解釈を与えられることになるのである。
。

