サルでもわかる量子論　第７回　～粒子でもあり、波でもある～

第７回　ド・ブロイの物質波　～粒子でもあり、波でもある～
1923年、日本では関東大震災のあった年である。この年、物理学の歴史では、それまでの「完成された」と思われていた古典物理学と別れを告げる決定的な出来事がふたつあった。
ひとつは、アメリカのコンプトンが行った、光電効果の拡張実験「コンプトン効果」である。以前説明したようにその結果は、光の粒子性を揺るぎないものとして証明したのであった。
ところが、ふたつめの出来事は、全く正反対の事象を示すものであった。なんと、電子は波である、と言い出した人がいたのだ。その人の名をド・ブロイという。この人は、フランスでも名門貴族のド・ブロイ一族の第７代公爵である。最初は、ソルボンヌ大学で、歴史学を勉強していたが、第１次大戦で、通信員としてエッフェル塔に配備されていたときに、物理に興味を持ったということである。
彼のすごいところはその柔軟な発想、逆転の発想にある。アインシュタインの「光量子仮説」やコンプトンの「コンプトン効果」から世の中では「波だとばかり思っていた光は実は粒子でもあったんだねぇ！」と騒いでいるときに、「波だと思っていた光が粒子の性質を持つのなら、粒子であると思っていた電子や陽子が波の性質を持ってもいいんじゃないかな？」と考えたのだ。
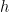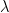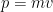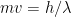ところで、これ以前、アインシュタインは「光が粒子の性質を持つのであるなら、運動量も持つはずだ！」と考え、光子の運動量 p=h/\lambda （h:プランク定数、\lambda:光の波長）と予想をし、それがコンプトン効果によって証明されていた。そこでボーアは「陽子や電子が粒子であるなら運動量 p=mv を持つはずであり、また同時に陽子や電子が粒子と波との二重性を持つなら、光と同じように運動量 p=h/\lambda を持つであろうと考え、 mv=h/\lambda となり、以下のようになる。
ド・ブロイの物質波　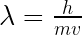 \lambda=\frac{h}{mv}
ちなみに光子の場合には質量をもたないので 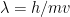\lambda=h/mv にはならないのだ。これはあくまでも、陽子や電子の場合だ。そして、この式が、先ほどのボーアの式につながるのだ！
まず、電子は原子核の周りをグルグル回っている。その円の長さは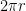 2\pi r だ。一方で、電子は波である！（と仮定している！）波ならば波長がある。波長を 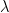\lambda としよう。波には、高い部分と低い部分、山と谷がある。もし電子が円の長さ 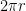2\pi r を1周して戻ってきたときに、この山と谷の位置がずれていたら円はつながらなくなってしまうのだ。また、別の説明をすると、山の位置と谷の位置が1周目と2周目でずれてしまうと波が弱くなり安定して存在することができないのだ。こうしてド・ブロイは、電子が波であると考えたとき、波の始まりと終わりが、円周上で一致するような波であると考えた。このためには、円周の長さを波長で割った値が割り切れる（つまり1、2、3、…）という整数になる必要がある。ではこれを式にしてみよう。 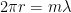2\pi r=m\lambda である。ところで先ほど述べたように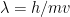\lambda=h/mv であるから、代入すると、 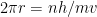2\pi r=nh/mv となり、さらに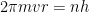2\pi mvr=nh となる。　
おや～？　そう、これはボーアの式と同じになるのだ！　ボーア自身は電子を波と考えて式を作った訳ではないのだが、その後、電子を波と考えたド・ブロイによって、ボーアの式は電子を波と考えていると解釈できるようになったのだ！　そして逆にド・ブロイの考えは、ボーアの電子モデルによって支持されるようになったのだ。
それはさておき、ところで、この考えは実におぞましいではないか？　だって、電子が波であるということは、原子が波であるということだ。原子が波であれば原子から成り立つすべてのものは波なんだ。そう、君も、僕も、机も、椅子も、この世のすべてが波なんだ！　これは狂っている！　でも、結局のところ証明されたことであれば、それに従わざるを得ない。
ド・ブロイが、この論文をパリ大学に提出したとき、パリ大学の理学部は、保守的すぎて、審判するのに躊躇した。そこで、アンシュタインを呼び出し、教えを請うた。アインシュタインは次のように答えたという。「これは狂気の沙汰と見えるかもしれない。しかし、真実、健全だ」。そして1927年、実際にド・ブロイ波（電子波）が発見され、ド・ブロイはノーベル物理学賞を受賞することになる。
これこそ、まさに、古典物理が崩れ去り、あらたな物理学「量子論」が誕生した瞬間である。