屋代高校１年　春休み宿題　図形問題

「１辺が6ｃｍの正方形において、真ん中の色つき部分の面積を求めなさい。」

この問題を解く際、必要なのが補助線。

補助線を２本付け足します。

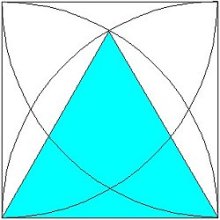
この三角形が正三角形だということはすぐに分かります。

１つの角は60°

ということで、

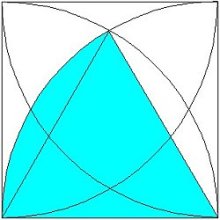
この扇形の面積を最初に求めます。

半径6ｃｍでなす角60°の扇形の面積は、普通に求められるでしょう。

次に、この扇形から先程の正三角形の面積をひくと、

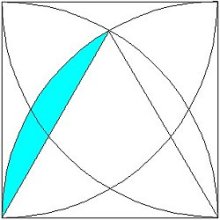
こんな形が出来あがります。

次に、

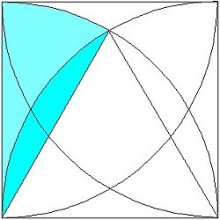
１辺が6ｃｍで、なす角30°の扇形の面積から、

先程出した細長い面積を引きます。

すると、残った図形の形は次のようになります。

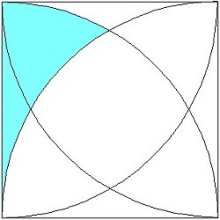
これを、１辺6ｃｍの正方形の面積から４つ引くことで

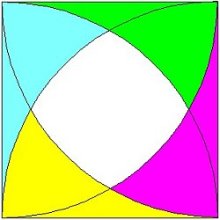
真ん中部分の面積を求められます。

解いてみて下さい。