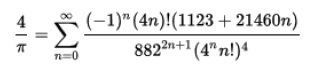
★天才か宇宙人か★
先日、数学の授業の際、ブラーマグプタの公式の話題から
ラマヌジャンの話題となりました
ラマヌジャンは、インド人の数学者で
彼の名を知っている人は、「数学通」かはたまた「雑学が好きな人」かぐらいで
一般の人はほとんど彼の名を聞いたことがないことでしょう
かく私もつい最近まで聞いたことがありませんでした
彼は「インドの魔術師」とも呼ばれ、32歳という若さで亡くなりました
が、その生涯で彼が発見した公式は数知れず、
しかも! その公式の多数が彼曰く「神から授かったもの」という話
実際、その公式をどのように導けば良いの彼自身も分からないほどという話だ
たとえば、次の公式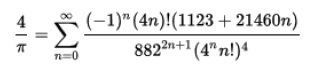
こんな複雑な公式を見つけるなんて、彼は天才かそれとも宇宙人なのか
未だに不思議な数学者として知られている

★受験勉強は慎重に★
季節はすっかり秋模様
朝夕はかなり寒くなり風邪も流行っている様子
各高校の沖縄修学旅行も終わり、今週から通常授業が再開となりました
次回の学校のテストは11月下旬で1か月以上先ということもあり
高校1年生や2年生にとってはまた普段と変わりない日常に戻ったことでしょう
一方、高校3年生にとっては
いよいよ「センター試験まで残り100日」を切り
気持ちがだいぶ焦り始める時期となりました
しかしながら、成績がなかなか上がらなくても
けっして焦って雑に勉強しないように心掛けることが大切です
特に時間がかかる科目の受験勉強には、”より慎重になるべき”で、
例えば数学の途中式の計算を雑に省略しすぎて書いてしまったり、
英語の単語や熟語を書かずに、解答だけ見て正解したと錯覚していまうなど
この時期再度自分の学習が雑になっていないか確認しておきたいところです

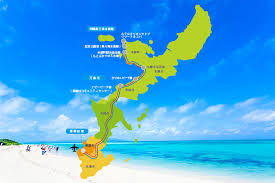
★はいさい沖縄★
毎年9月下旬から11月にかけて
各高校の修学旅行の時期になります
今週は、篠ノ井高校2年生が沖縄へ修学旅行へ出かけている最中で
来週は長野西高校、そしてその翌週には屋代高校と続きます
この近隣の高校の修学旅行と言えば、毎年「沖縄」で
沖縄地元の家庭にも泊まる「民泊」もあり、
修学旅行前の塾生たちに話を聞くと、
「もうワクワクが止まらない!」とのこと
今週は天気も良さそうで
きっと修学旅行を楽しんでいる頃でしょう
その修学旅行で毎年訪ねる場所があるそうで
それが「美ら海水族館」
中でもジンベエザメが圧巻とのこと
大阪にある「海遊館」にもいるので
長野からジンベエザメを見に行くなら大阪の方が近くて良いかも
ジンベエザメで思い出しましたが、
今年の夏は息子たちとジンベエザメ浮輪を持ってプール遊びに行きました そんな楽しい夏も終わり、季節はこれから秋
そんな楽しい夏も終わり、季節はこれから秋
庭の金木犀から良い香りがし始める季節になりました
センター試験まで残り、4ヵ月
「学習の秋」スタートです

★Hallowe’en★
9月も後半になり、ちょっと早いですが、
塾生の入退室用PC画面をハロウィン用に変えました
お菓子も少しだけ今から用意しておこうかな、と。

★虹★
この時期、雨上がりに虹が見られますが
虹の語源が気になって調べてみました
英語で、虹は「rainbow」と言いますが、
調べてみたら簡単なことでした、
読んで字の如く「雨+弓」で「rainbow」
確かに雨上がりに弓のような形で見られますしね
では、なぜ日本語では「にじ」と言うのでしょうか
これも少しだけ調べてみました
一説によると、「にじ」は「長虫」を意味する「なじ」や「なが」が由来とのこと
この「なじ」や「なが」が次第に「ぬじ」「のじ」と変化し
最終的に「にじ」になったということらしい
「虹」という漢字に「虫」を使うのもこの言葉が由来だからなのでしょう


★高校文化祭★
6月のテストが終わり7月になるとすぐに高校の文化祭があります
今年はどの高校も7月1週目の土日が文化祭となっており
生徒によってはクラス展の準備やクラスのダンス練習で
テスト勉強とともにかなり忙しい時期になっています
ところで、この文化祭が行われるようになったのは
昭和26年頃のことだそうで
当初は、生徒の有志が文化人を招いたり、
書道や絵画を展示する簡素なものだったそうです
それが、1960年代の受験戦争時期になると次第に寂れ、
学生運動時には文化祭自体が行われないこともあったようです
ところで、文化祭と言えば秋に行うイメージがありませんか?
当初行われていた文化祭は、基本的には秋に行われていました
理由は、いたって普通
・11月に文化の日があるから
・気候的に行いやすい季節だから
だそうです
ところで長野の高校文化祭が7月にあるのはなぜなんでしょうかね
きっと理由があるはずですが

★七面鳥★
今年もそろそろ梅雨入りの模様
新元号になって初めての梅雨入りですが、例年並みらしいです
ごきげんよう
只今各高校とも6月下旬に学校テスト準備、
7月の文化祭準備さらにはクラスマッチや部活の大会などなど
行事が盛り沢山でかなり忙しい時期です
日中と夜の寒暖差も大きいため、体調には十分気を付けたい
そんな梅雨入り間近
さて、梅雨と言えば紫陽花 紫陽花の語源は、「藍色が集まったもの」を意味する
紫陽花の語源は、「藍色が集まったもの」を意味する
「あづさい(集真藍)」がなまったものが有力な説のようです
ちなみに万葉集には紫陽花が詠まれた和歌が2首収録されています
第四巻 773番 大伴家持
言問はぬ 木すら味狭藍 諸弟らが 練りの村戸に あざむかえけり
第二十巻 4448番 橘諸兄
安治佐為の 八重咲くごとく 八つ代にを いませ我が背子 見つつ偲ばむ
「色が移り変わる花」や「幾重にも重なって咲く花」としてその昔から
親しまれていたようですね
さらには、七面鳥の肌の色が変わることに喩え、
新潟県や佐賀県では、紫陽花のことを「七面鳥」と呼ぶこともあるらしいです
![IMAG0003[1]](http://www.5kaku.net/wordpress/wp-content/uploads/2018/09/IMAG00031.jpg)
★6月テストだ★
先週、高校のテストが終わり今週からテスト結果が返却され始めました
塾生に少し話を聞くと、数学αで90点以上取れていたりと
なかなか点数が良かった模様
・・・ですが、
次回のテストまで残り1カ月切りました
今度のテストは6月下旬です
しかも今度のテストは、出題範囲も広くなり
今回平均点が高かった科目は次回のテストで平均点がかなり下がると予想されます
今から少しずつ準備をしておかないと点数を大幅に下げてしまうことになってしまいます
今週末からまた気を引き締めてテスト準備を開始しましょう
<高校 6月テスト日程>
屋代高校 定期考査① 6/24.25.26
篠ノ井高校 期末考査 6/24.25.26
文化学園 期末考査 6/25.26.27
長野南高校 期末考査 6/19.20.21
![IMAG0003[1]](http://www.5kaku.net/wordpress/wp-content/uploads/2018/09/IMAG00031.jpg)
長いゴールデンウィークが終わり
高校によっては来週にはテストがあります
高校1年生にとっては、初めての高校内容のテストになります
出題範囲は狭いですが、今後の学校試験の出題のされ方も分かるため
テストが終わった後に必ず解き直しをしておき
次回のテストにその経験を活かしていってもらいたいところです
<高校テスト日程>
屋代高校 5/16.17
篠ノ井高校 5/22.23.24
長野西高校 5/21.22.23
文化学園 5/21.22.23
長野南高校 5/15.16.17

 4月も中旬となりだいぶ暖かくなりました
4月も中旬となりだいぶ暖かくなりました
桜も満開になったこの時期
自宅の庭にトマトの苗を植えました
ところで、ご存知でしょうか
トマトと一緒に植えると良いと言われている植物があります
1.ネギやニラ
ニラやネギの苗をトマトの根とくっつくように植えるんだそうです。
こうすることで、トマトがかかりやすい病害虫を予防してくれるとのこと。
2.パセリ
パセリもトマトの株元近くで植えて
一緒に育つことで、パセリがトマトの害虫を予防してくれるという。
3.バジル
トマトとバジルを植えた土が湿り、トマトが必要とする以上に水分がある時、
バジルが余分な水分を吸うため、トマトが育ちやすい乾燥具合が保てるとのこと。料理でもトマトとバジルの相性はバッチリですね。
4.アスパラガス
トマトは連作をしていると、センチュウによる被害が出やすくなり、
接ぎ木苗を使っても、センチュウ被害に合えば生育が悪くなってしまうとのこと。アスパラガスはそのセンチュウそのものを予防してくれるという。
5.マリーゴールド
マリーゴールドもセンチュウ被害を予防してくれるハーブで知られています。
というわけで、今年はネギと一緒にトマトを植えてみました。