◆平成25年度長崎県 数学 超難問(正答率1.7%) 解答と解説
正の偶数を 2n とする。
2つの続いた正の偶数は 2n , 2n+2 と表すことができる。
「ある2つの続いた正の偶数の平方の和から2を引いた数」は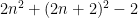 となる。
となる。
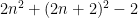
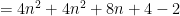


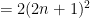
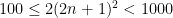
 ・・・①
・・・①
2つの続いた正の偶数は 2n , 2n+2 と表すことができる。
「ある2つの続いた正の偶数の平方の和から2を引いた数」は
この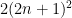 が3ケタの 7 の倍数になるので、
が3ケタの 7 の倍数になるので、
ここで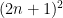 は 7 の倍数、かつ、奇数である・・・②
は 7 の倍数、かつ、奇数である・・・②
①と②の両方を満たすのは、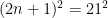 である。
である。
ゆえに、 なので
なので 
そこで、2つの続いた正の偶数は 2n , 2n+2 は、それぞれ 20 , 22 となる。
答え.20 , 22

