◆平成25年度岐阜県　数学　超難問(正答率0%)　解答と解説
三角形△ABH と 三角形△ACDで、弧ADに対する円周角は等しいので、
角∠ABH ＝ 角∠ACD
問題文より、角∠AHB ＝ 90°
半円の弧に対する円周角は 90° になるので、
角∠ADC ＝ 90°
以上より 角∠AHB ＝ 角∠ADC
よって、２組の角がそれぞれ等しいので、
三角形△ABH ∽相似 三角形△ACD となる。角∠ADC は直角である。
三角形△ACD は直角三角形なので、三平方の定理により　AD = 8 (cm)
角∠EAH = 角∠DAH より 三角形△AED は二等辺三角形なので AE = AD = 8 (cm)ところで、三角形△ADH は直角三角形なので 角∠DAH ＋ 角∠ADH = 90°
一方　角∠ADH ＋ 角∠BDC = 90°　なので　角∠DAH = 角∠BDC

円周角は等しいから 角∠BDC = 角∠BAC
これらから　三角形△ABH で 角∠BAE = 角∠EAH となり、辺AE は角の二等分線となるから
BE : EH = AB : AH = AC : AD = 10 : 8 = 5 : 4
そこで BE = 5x とすれば EH = 4x で BH = 9x となる。

BH : AH = CD : AD = 6 : 8 = 3 : 4 だから AH = 12x
三角形△AEH は直角三角形で AE = 8 , EH = 4x , AH = 12x だから、三平方の定理で x が求まり、BE が求まる。

答え　ルート√10

 

◆平成26年度青森県（前期）　数学　超難問(正答率0.0%)　解答と解説
（１）ア　　\frac{S}{4}
（１）イ　　\frac{S}{4}+\frac{S}{6}=\frac{3S}{12}+\frac{2S}{12}=\frac{5S}{12}=
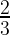（２）　最初の４０分　　\frac{2}{3}時間　→　二人なのでの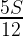\frac{5S}{12}　→　積が二人で最初に塗った面積
　　　　残り時間　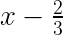　x-\frac{2}{3}時間　→　ユウさん一人なのでの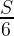\frac{S}{6}　→　積がユウさんが次に塗った面積
　　　　塗り終わった面積　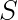　S
　　　　ゆえに、\frac{2}{3}\times \frac{5S}{12} + (x-\frac{2}{3}) \times \frac{S}{6} = S

　

　　　　以上を解いて　　x=5
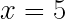
（２）　ケンさんがユウさんに教える時のケンさん　\frac{S}{4}\times \frac{9}{10}
　　　　ケンさんがユウさんに教える時のユウさん　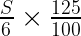\frac{S}{6}\times \frac{125}{100}
　　　　ケンさんがユウさんに教える時の二人の合計　\frac{S}{4}\times \frac{9}{10}+\frac{S}{6}\times \frac{125}{100}
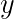　　　　最初の時間　y　→　ユウさん一人なのでの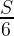\frac{S}{6}　→　積がユウさんが最初に塗った面積
　　　　残り時間　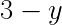　3-y時間　→
　　　　 ケンさんがユウさんに教えている時の二人なので\frac{S}{4}\times \frac{9}{10}+\frac{S}{6}\times \frac{125}{100}

　

　　　　 →　積がユウさんが次に塗った面積
　　　　塗り終わった面積　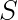　S
　　　　ゆえに、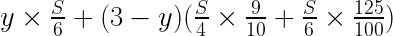y \times \frac{S}{6} + (3-y)(\frac{S}{4}\times \frac{9}{10}+\frac{S}{6}\times \frac{125}{100})

　

　　　　以上を解いて　　y=\frac{9}{8}