◆ラサール高校 数学 難問 解答と解説
(1)
自力でも解けるが、素因数分解を利用して素数の和を調べる方法を知っていれば時間を短縮できる。
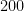 を素因数分解すると、
を素因数分解すると、
よって、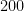 の約数の和は、
の約数の和は、
 これを素因数分解するので、
これを素因数分解するので、
自力でも解けるが、素因数分解を利用して素数の和を調べる方法を知っていれば時間を短縮できる。
よって、
(2)





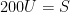
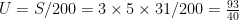


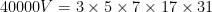

(3)
両辺に をかける。
つまり、右辺はSの式を逆の順序にしたものでSと同じ。
(4)
Vの両辺に をかける。
つまり、右辺はVの式を逆の順序にしたものでVと同じ。
