◆開成高校 数学 難問 解答と解説
(1)点Bの座標を  とすると、傾きの公式より
とすると、傾きの公式より 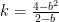 となる。因数分解すると、
となる。因数分解すると、 となる。よって、
となる。よって、 となるので、点Bの座標は
となるので、点Bの座標は  となる。
となる。
(2)(1)の点Bの座標と点Aの座標 が一致すればよいので、  より
より  となる。点A
となる。点A  を通り、傾き
を通り、傾き  なので、
なので、 に代入して
に代入して 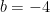 。ゆえに求める式は
。ゆえに求める式は 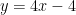 となる。
となる。
(3)
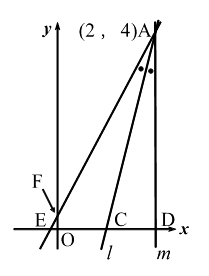 線
線 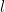 が
が  なので、点Cの座標が
なので、点Cの座標が  とわかる。ここで点Eの座標を
とわかる。ここで点Eの座標を  とおくと、三平方の定理より
とおくと、三平方の定理より 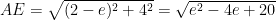 となる。
となる。
一方で、図より が成り立つので
が成り立つので


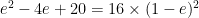



図より
直線AEは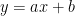 に点A
に点A  点E
点E 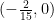 を代入して、
を代入して、 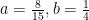 となるので、点Fは
となるので、点Fは 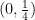
 線
線 一方で、図より
図より
直線AEは
