フィボナッチ数列
昨日の数学Ⅲの授業で、たまたま隣接三項間漸化式からの極限を扱い
その際、少し時間が余ったので、
フィボナッチ数列を話題として取り上げてみました
1 1 2 3 5 8 13 21 …
と変化していく数列のことを特にフィボナッチ数列と呼びます
このフィボナッチ数列には面白い特徴があり、
知っている人も多いですが「黄金比」がこの数列の中に隠されています
具体的に言うと、前の数字と次の数字の比率が、
最終的に黄金比率である「1.618…」という数字に近づいていきます
例えば、
1 → 1 (1倍)
1 → 2 (2倍)
2 → 3 (1.5倍)
3 → 5 (1.66…倍)
5 → 8 (1.6倍)
8 → 13 (1.625倍)
・・・・・・(1.618…倍)というように変化していきます。
この時に現れる1.618という数字が自然界の中のあらゆる場面で見ることができ、
自然界の中ではこの比率が最も美しい比率として知られています。
例えば、植物の葉の開き方やオウムガイの断面図、ひまわりの種などなど


ひまわりの種は螺旋状になっており、ここのフィボナッチ数列が見られます
そしてその黄金比率を使った有名な絵画が、レオナルドダヴィンチが描いた「モナリザ」

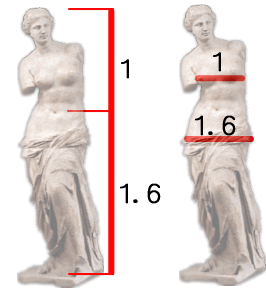
建造物ではパルテノン神殿や、
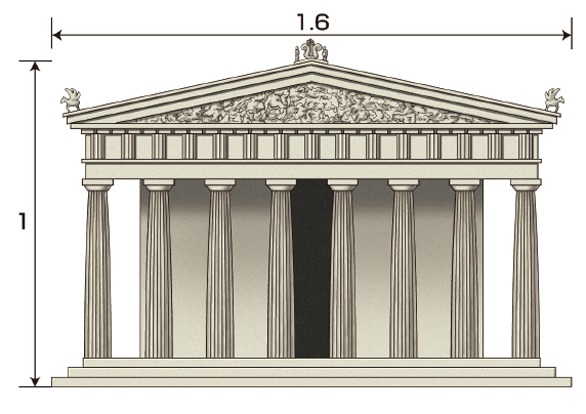
ミロのヴィーナスなどにも黄金比率が見られるそうです
また、五芒星の中にも黄金比率が見られるため
古より人々はその記号を特別な記号として崇め
あらゆる場面、例えば勝利した際の記号として、
または国旗の記号として、時には魔術の魔法陣等、様々な場面で使用してきました。
そのフィボナッチ数列の漸化式は、次の通りです
F0 = 0
F1 = 1
Fn + 2 = Fn + Fn + 1 (n ≧ 0)