入試問題に挑戦! 平成12年 青森県 (やや難)
平成12年度 青森県 数学 第5問 (2) 難易度・・・やや難
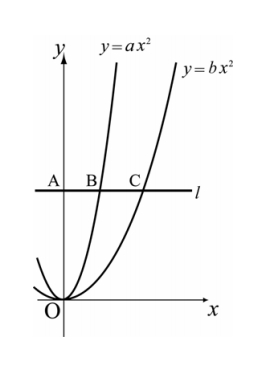
上の図のように、 軸に平行な直線
軸に平行な直線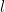 が、
が、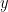 軸、関数
軸、関数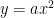 のグラフ、関数
のグラフ、関数 のグラフと交わる点
のグラフと交わる点
をそれぞれ

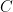 とする。
とする。
をそれぞれ
ただし、点 と 点
と 点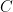 の
の  座標はともに正の数とする。
座標はともに正の数とする。
↓
↓
↓
↓
↓
解説解答はコチラ
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
これは、どの座標に注目をして日だ作るか、つまりどこに媒介変数を使うかで少し悩みます。
今回は  の
の  座標を
座標を 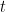 とおいて考えます。(
とおいて考えます。(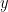 座標を
座標を 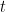 としても出せます。)
としても出せます。)
それぞれの式に代入し、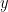 座標を求めると、
座標を求めると、 、
、 と表せます。
と表せます。
つまり  は
は 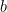 の
の 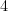 倍ですから、
倍ですから、 となります。
となります。
正解 

