入試問題に挑戦! 平成27年 神奈川県 (超難)
平成27年度 神奈川県立高校入試 数学
(ア)(イ)もなかなか難しいのですが、特に(ウ)は難関私立高入試レベルです。
入試本番であれば、(ウ)は捨てて、他の問題を考えたり、他の問題の見直しをする方がいいかもしれませんね!
では頑張って解いてみてください!

↓
↓
↓
↓
↓
解説解答はコチラ
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
問6 (空間図形)
(ア)
円すいの高さ  は、
は、 となり、
となり、
よって、円すいの体積は、
(イ)
2点  を含む平面
を含む平面 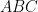 で考える。
で考える。
点 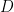 から下ろした垂線と線分
から下ろした垂線と線分 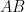 の交点を点
の交点を点 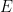 とすると、
とすると、
中点連結定理より、 、
、 となる。
となる。
三平方の定理より、
(ウ)
表面上の最短距離なので、円すいの側面で考える。
側面のおうぎ形の中心角は、
最短距離より、図1の AA’ が求めたい線になる。
△ACA’ はおうぎ形の半径から,頂角 108°、底角 36°の二等辺三角形。
∠ACA’を 36°と 72°になるように分割した線と AA’の交点を F とすると、図 2 のようになる。
求めたい AA’を xcm とすると AF=(x-10)cm となる。
△ACA’∽△AFC より、 10:x=(x-10):10、 ゆえに、 となり、
となり、
x>0 より、

