高校入試への数学(1) 一次関数① 対称な点
時習館の森山の
 高校入試への数学
高校入試への数学
~第1講 一次関数① 対称な点~
【問題】 (難易度★★☆☆☆)
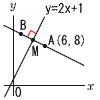
直線 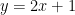 に関して、点
に関して、点 
 と対称な点
と対称な点  の座標を求めなさい。
の座標を求めなさい。
↓
↓
↓
↓
↓
 【ズバリPoint!】
【ズバリPoint!】直線 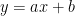 に関して、点
に関して、点  と点
と点  が対称な位置にある場合
が対称な位置にある場合
→ ① 直線 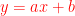 と直線
と直線  は直交する
は直交する
→ ② 直線 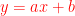 と直交する直線の傾きは
と直交する直線の傾きは  になる
になる
→ ③ 直線 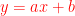 は直線
は直線  の中点を通る
の中点を通る
↓
↓
↓
↓
↓
【解答と解説】
求める点  の座標を
の座標を 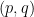 とすると、
とすると、
直線 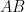 は
は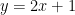 と直交するので、
と直交するので、
直線 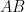 の傾きは
の傾きは  になればよい。
になればよい。
この式を整理して、 ・・・ ア
・・・ ア
また、直線 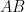 nの中点
nの中点 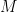 の座標は、
の座標は、 になる。
になる。
この中点 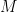 は、直線
は、直線 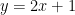 のうえにあるので、代入すると、
のうえにあるので、代入すると、
この式を整理して、 ・・・ イ
・・・ イ
アとイより連立方程式を解くと、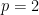 ,
,  となる。
となる。
答え  ,
, 

