高校入試への数学(2) 一次関数② 交点と面積
時習館の森山の
 高校入試への数学
高校入試への数学
~第2講 一次関数② 交点と面積~
【問題】 (難易度★☆☆☆☆)
下の図で、直線 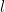 は関数
は関数 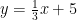 のグラフ、直線
のグラフ、直線 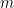 は関数
は関数 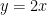 のグラフ、直線
のグラフ、直線  は関数
は関数 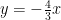 のグラフ、ある。直線
のグラフ、ある。直線 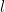 と直線
と直線 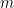 は点
は点  で、直線
で、直線 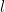 と直線
と直線  は点
は点  でそれぞれ交わっている。ただし、原点
でそれぞれ交わっている。ただし、原点 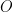 から点
から点 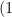 ,
,  までの距離、及び原点
までの距離、及び原点 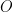 から点
から点 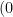 ,
,  までの距離をそれぞれ
までの距離をそれぞれ  とする。
とする。
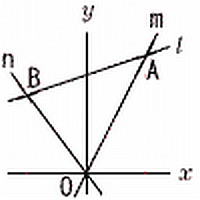
(1) 点  の座標を求めなさい。
の座標を求めなさい。
(2) △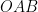 の面積を求めなさい
の面積を求めなさい
(3) △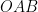 を、原点
を、原点 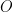 を回転の中心として時計の針の回転と反対の向きに、辺
を回転の中心として時計の針の回転と反対の向きに、辺 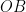 が初めて
が初めて 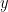 軸に重なるまで回転移動した。点
軸に重なるまで回転移動した。点  が移った点を
が移った点を 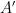 とするとき、点
とするとき、点 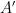 の座標を求めなさい。
の座標を求めなさい。
↓
↓
↓
↓
↓
 【ズバリPoint!】
【ズバリPoint!】 → 直線 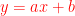 ・・・①と 直線
・・・①と 直線  ・・・② の交点
・・・② の交点  を求めるときは、 ①と②を連立方程式にし求める。
を求めるときは、 ①と②を連立方程式にし求める。
↓
↓
↓
↓
↓
【解答と解説】
(1)
点  は、直線
は、直線 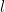 と直線
と直線 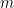 の交点になるので、
の交点になるので、
直線 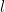 :
: 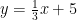 …①
…①
直線 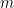 :
: 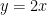 …②
…②
①と②を連立方程式で解くと、 、
、 となる。
となる。
答 点 
 ,
, 
(2)
まず点  の座標を考える。
の座標を考える。
点  は、直線
は、直線 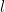 と
と  は関数
は関数 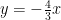 の交点になるので、
の交点になるので、
直線 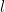 :
: 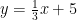 …①
…①
直線  :
: 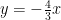 …②
…②
①と②を連立方程式で解くと、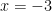 、
、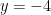 となる。
となる。
点 
 ,
, 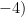
次に、左図のように、「正方形-まわりの3つの三角形」で考える。
△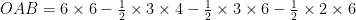
答 
(3)
△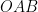 回転すると、左図のようになる。
回転すると、左図のようになる。
ここで、 、
、 とすると、
とすると、
図より、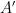 の座標は
の座標は 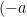 ,
,  になる。
になる。
答 点 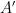
 ,
,