高校入試への数学(4) 平方根の小数部分
時習館の森山の
 高校入試への数学
高校入試への数学
~第4講 平方根の小数部分~
【問題】 (難易度★★☆☆☆)
↓
↓
↓
↓
↓
 【ズバリPoint!】
【ズバリPoint!】平方根の小数部分の求め方
ポイント1:整数を平方根の形にして、与えられた平方根との大小関係から、整数部分を考える。
ポイント2:平方根の小数部分 = 平方根-整数部分
因数分解の応用
ポイント: =
=  =
= 
上記の式変形は高校数学ではよく出てくるので覚えておくと便利!
↓
↓
↓
↓
↓
【解答と解説】
ゆえに  なので、
なので、
よって、 の整数部分を
の整数部分を  となり、
となり、
ゆえに、 なので、
なので、 となる。
となる。
以上より整数部分 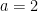 、小数部分
、小数部分  となる。
となる。
ここで、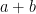 =
=  =
=  となる。
となる。
また、 =
=  =
=  である。
である。

