ワカるデキる 対数(2) ~足し算にすればラク~
前回、暗号表を使って以下の問題を解くように述べたが、出来たであろうか?
まずは1番目の問題で考えてみよう。これは暗算で解けるね。 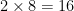 だ。
だ。
このとき、暗号表の対応を考えてみると、“数字2″に対応するのが”暗号1″、”数字8″に対応するのが”暗号3″、”数字16″に対応するのが”暗号4”だ。数字では “2” “8” “16” の関係は 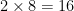 という掛け算になっているが、暗号では “1” “2” “4” の関係が
という掛け算になっているが、暗号では “1” “2” “4” の関係が  という足し算になっているね。ここが重要!
という足し算になっているね。ここが重要!
次に2番目の問題で確かめてみよう。  という問題だ。”数字32″に対応するのが”暗号5″、”数字64″に対応するのが”暗号6″だ。数字では掛け算だが、暗号では足し算になるはずだから、
という問題だ。”数字32″に対応するのが”暗号5″、”数字64″に対応するのが”暗号6″だ。数字では掛け算だが、暗号では足し算になるはずだから、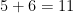 となり、”暗号11″に対応する数字になるはずだ。ということで”数字2048″になる。数字の計算で確かめてみよう。うん、ちゃんとあってるね!
となり、”暗号11″に対応する数字になるはずだ。ということで”数字2048″になる。数字の計算で確かめてみよう。うん、ちゃんとあってるね!
同様に3番目の問題  の数字を暗号化して足し算にすれば、
の数字を暗号化して足し算にすれば、  となり、数字化すれば 8192 になる。
となり、数字化すれば 8192 になる。
4番目の問題も 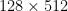 の数字を暗号化して足し算にすれば、
の数字を暗号化して足し算にすれば、  となり、数字化すれば 65536 になる。
となり、数字化すれば 65536 になる。
このように掛け算のしくみを足し算に変換できれば計算が楽になるね。この考え方が対数への第1歩なんだ。
ちなみに、この暗号表の暗号は何かわかるかい? そう、君たちももう気付いていただろうけれど、この暗号は指数なんだ。実は対数は指数ととても深いかかわりを持っている。
では、そのお話は次回することにしよう!
