入試問題に挑戦! 開成高校 数学 難問
開成高校の入試問題です。
ひらめきというよりも、力技でグイグイ押し込む力が必要になります。 頑張って解いてみよう!
===
放物線 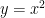 上の点A
上の点A  を通る直線
を通る直線 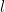 を考える。ただし
を考える。ただし 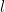 は
は 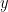 軸に平行でないものとする。
軸に平行でないものとする。
(1)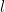 と
と 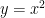 とが、点A以外の点Bをも共有しているとき、直線
とが、点A以外の点Bをも共有しているとき、直線 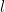 の傾き
の傾き 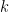 を用いて点Bの座標を表せ。
を用いて点Bの座標を表せ。
(2)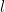 と
と 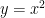 とが、点A以外で共有点をもたないとき、直線
とが、点A以外で共有点をもたないとき、直線 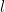 を表す方程式を求めよ。
を表す方程式を求めよ。
(3)(2)で求めた直線 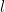 に対し、
に対し、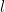 と
と  軸との交点を 点C とする。また、点A を通り
軸との交点を 点C とする。また、点A を通り 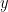 軸と平行な直線を
軸と平行な直線を 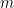 とし
とし 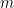 と
と  軸との交点を 点D とする。さらに 角∠CAE = 角∠CAD となるように点D と異なる
軸との交点を 点D とする。さらに 角∠CAE = 角∠CAD となるように点D と異なる  軸上の点E をとる。 このとき、直線AE と
軸上の点E をとる。 このとき、直線AE と 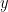 軸との交点を 点F とするとき、点F の座標を求めよ。
軸との交点を 点F とするとき、点F の座標を求めよ。
