高校入試への数学(3) 一次関数③ 比と中点
時習館の森山の
 高校入試への数学
高校入試への数学
~第3講 一次関数③ 比と中点~
【問題】 (難易度★★☆☆☆)
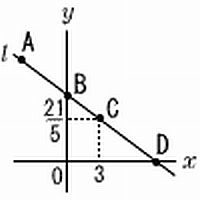
右の図のように、直線 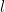 上に異なる4点
上に異なる4点  、
、 、
、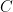 、
、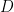 があり、
があり、 、
、 が成り立っている。点
が成り立っている。点 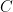 の座標が
の座標が ,
, であるとき、それぞれ以下の問題に答えよ。ただし、原点を
であるとき、それぞれ以下の問題に答えよ。ただし、原点を 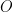 とする。
とする。
(1) 点  の座標を求めなさい。
の座標を求めなさい。
(2) 点  を通り、△
を通り、△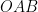 の面積を二等分する直線の式を求めなさい。
の面積を二等分する直線の式を求めなさい。
↓
↓
↓
↓
↓
 【ズバリPoint!】
【ズバリPoint!】連比の求め方(二つの比を一つにまとめる)
ポイント: の値を最小公倍数で同じ数にそろえる。
の値を最小公倍数で同じ数にそろえる。
例題: …①
…①  …② のとき、二つの比を一つにまとめよ。
…② のとき、二つの比を一つにまとめよ。
解法:①式では 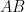 の値は
の値は 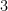 、②式では
、②式では  の値は
の値は 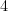 なので、最小公倍数の12になるように、①式に
なので、最小公倍数の12になるように、①式に 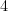 をかけ
をかけ  …①’、②式に
…①’、②式に 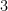 をかけ
をかけ  …②’となる。また①’②’より、
…②’となる。また①’②’より、 、
、 なので、
なので、 になる。
になる。
中点座標の求め方
ポイント:点  ,
, と 点
と 点  ,
, を結ぶ線分
を結ぶ線分  の中点
の中点  の座標は、
の座標は、 ,
, になる。
になる。
↓
↓
↓
↓
↓
【解答と解説】
(1)
点  から降ろした垂線が
から降ろした垂線が  軸と交わる点を
軸と交わる点を 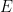 、点
、点 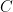 から降ろした垂線が
から降ろした垂線が  軸と交わる点を
軸と交わる点を 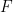 とし、また点
とし、また点  から降ろした垂線が
から降ろした垂線が  軸と交わる点は
軸と交わる点は 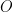 であり、点
であり、点 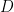 は
は  軸上にある点であるので、△
軸上にある点であるので、△ 、△
、△ 、△
、△ はそれぞれ相似の直角三角形である。
はそれぞれ相似の直角三角形である。
点  の座標を
の座標を  ,
, 、点
、点  の座標を
の座標を 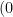 ,
, 、点
、点 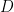 の座標を
の座標を  ,
, 、とする。
、とする。
点  の
の  座標は
座標は  、点
、点  の
の  座標は
座標は 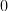 、 点
、 点 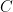 の
の  座標は 3[/latex]、
座標は 3[/latex]、 なので、点
なので、点  の
の  座標は
座標は  になる。
になる。
同様に、点  の
の 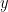 座標は
座標は 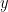 、点
、点 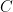 の
の 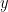 座標は
座標は 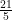 、 点
、 点 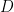 の
の 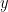 座標は 0[/latex]、
座標は 0[/latex]、 なので、点
なので、点 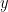 の
の  座標は
座標は 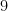 になる。
になる。
よって、点 
 ,
,
(2)
同様に点  の座標を求めると、
の座標を求めると、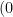 ,
, となる。
となる。
△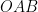 の面積を二等分するためには、底辺となる線分
の面積を二等分するためには、底辺となる線分 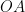 を二等分する中点
を二等分する中点 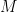 を通れば良い。
を通れば良い。
線分 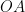 の中点
の中点 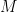 の座標を
の座標を  ,
, とすると、
とすると、 、
、 となる。
となる。
ゆえに、点 
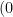 ,
, と 中点
と 中点 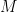
 ,
, の二点を通る線分を求める。
の二点を通る線分を求める。
それぞれの座標の  と
と 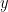 を
を 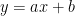 に代入して連立方程式で解く。
に代入して連立方程式で解く。
よって、