高校入試への数学(5) 根号の計算の応用
時習館の森山の
 高校入試への数学
高校入試への数学
~第5講 根号の計算の応用~
【問題】 (難易度★☆☆☆☆)
次の二次方程式を解きなさい。
(1) 
(2) 
(3) 
↓
↓
↓
↓
↓
 【ズバリPoint!】
【ズバリPoint!】根号を含む計算の工夫の仕方
ポイント1:共通因数をくくりだして整理する。
ポイント2:展開公式  =
=  を利用する。
を利用する。
例題:
= 
= 
= 
= 
= 
= 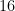
ポイント3:分母に  がある時には、
がある時には、 を掛けて、分母を有理化する。
を掛けて、分母を有理化する。
例題:
= 
= 
= 
= 
= 
= 
↓
↓
↓
↓
↓
【解答と解説】
(1)
= 
= 
= 
= 
= 
(2)
= 
= 
ここで、 、
、 を戻すと、
を戻すと、
= { }{
}{ }
}
= 
= 
(3)
= 
= 
= 
= 
{ }{
}{ 、
、
= 
= 
=